Recently for work, I've been experimenting with PyMC3.

In particular, I was toying with this example which shows how to implement Gaussian Mixture Models. My goal was to to a generalized mixture, using Gamma distributions instead of more classical Normal distributions.

At the end of my calculations, I wanted to plot the resulting distributions, along with each component:

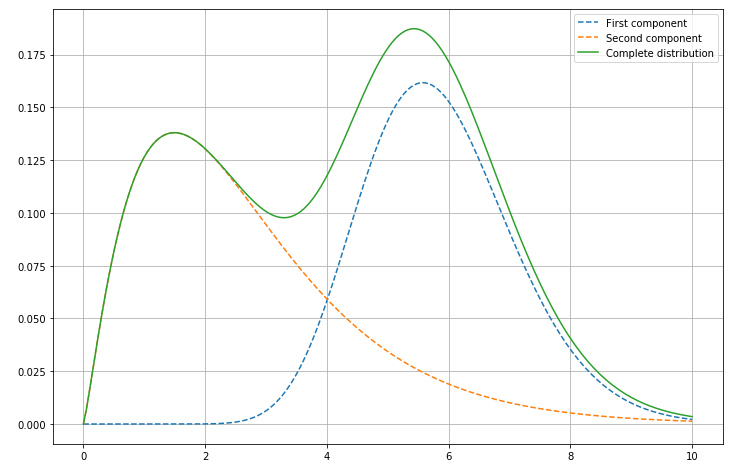
To plot this, I just had to get the average parameters for each Gamma distributions, and compute the probability density function of each component and of the weighted sum with scipy.stats.gamma. Easy, right?

Wrong.

Because the samples you get from your MCMC chain make it easy to compute the mean $\mu$ and standard deviation $\sigma$ of each Gamma distribution, but it is not so straightforward to parametrize Gamma distributions in scipy.stats with $\mu$ and $\sigma$.

Canonical formulation vs. API consistency¶

If you refer to the definition of the Gamma distribution, it is defined in its canonical form by a shape parameter $k$ and a scale parameter $\theta$.

The mean and standard deviation of the distribution are related to these parameters by a nice, simple formulas:
$\begin{equation} \mu = k\theta \\ \sigma^2 = k\theta^2 \\ \end{equation}$

From here, it's easy to obtain the formulas for $k$ and $\theta$:
$\begin{equation} k = \frac{\mu^2}{\sigma^2} \\ \theta = \frac{\sigma^2}{\mu} \\ \end{equation}$

The problem is that scipy.stats does not use the canonical parameters in its formulation of usual distributions, but a combination of two parameters loc and scale with some additional parameters depending on the distributions.

For instance, to parametrize the Normal distribution you have to plugin the mean $\mu$ as the loc parameter, and the standard deviation $\sigma$ as the scale parameter, which feels quite natural.
But to parametrize a Gamma distribution, a new parameter a appears, whereas for a Beta distribution, two parameters a and b appear alongside loc and scale.

Parametrizing a new distribution is thus a bit more complicated as you have to check the documentation.

So what's arguably good for API consistency is more confusing than not when it comes to clarity and ease-of-use.

There's a library for that¶

While googling around to better wrap my head around this, I found a helpful blog post describing this situation, and even presenting a small package, distcan, that rewrites the constructor of usual distributions and uses the canonical parametrization, making it easier not getting lost.

Whining about open-source code¶

In the end, it wasn't that much of a big deal, but it's always annoying to be stopped in your analysis and lose time on minor technicalities.
I know grumbling is easy and totally warrants a "Do it yourself if you're so unhappy" answer. But when your library features all kind of small friction points like this, you're probably hindering adoption by newcomers.

So I think a nice add could be to have a .from_mean_and_variance() static method to compute canonical parameter values when a closed-form expression exists. I'll try to make a PR on the distcan lib in the coming days to see how it goes.